Un San Valentín Matemático.

Desde el magnífico blog GAUSSIANOS os traigo un post muy especial para este día de los Enamorados. Disfrutadlo de todo corazón:

-----------------------------------------------------------------


Los sentimientos, y concretamente el amor, son de las pocas cosas de nuestra vida en las que la influencia de las matemáticas no es muy grande. No se puede explicar matemáticamente el amor, pero sí podemos demostrarlo utilizando las matemáticas. Demostrar el amor mediante, por ejemplo, un poema, está ya muy visto y generalmente no impresiona demasiado.

¿Qué mejor forma de demostrar nuestro amor entregando nuestro corazón? ¿Entregamos entonces un dibujo para ello? Demasiado imperfecto. Mejor que un programa de ordenador lo haga por nosotros, ya que así evitamos los errores (sabemos que no siempre es así, pero para el caso que nos ocupa nos sirve). Vamos a ver cómo el programa Mathematica nos puede ayudar a ello.
¡Demostremos nuestro amor!

Amor en 2-D

Vamos a dibujar un corazón solapando las siguientes curvas, que son las que vamos a utilizar en todo este apartado:

(parte del dibujo contenida en el semiplano superior)
(parte del dibujo contenida en el semiplano inferior)

Para representarlas en Mathematica introducimos el siguiente código:

f[x_]:=Sqrt[1-(Abs[x]-1)^2];
g[x_]:=ArcCos[1-Abs[x]]-Pi;
Plot[{f[x],g[x]},{x,-2,2},AspectRatio->Automatic]

El resultado es el siguiente: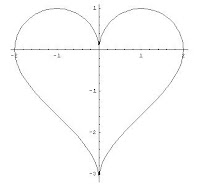




Corazón en 2D

Queda bonito…pero se puede mejorar. ¿Qué mejor que un corazón rojo? Y mejor con un trazo más ancho…y si se pudieran quitar los ejes sería perfecto. Ahí va:

Plot[{f[x],g[x]},{x,-2,2},AspectRatio->Automatic,PlotStyle-> {{RGBColor[1,0,0],Thickness[0.05]},{RGBColor[1,0,0],Thickness[0.05]}},Axes->False]

Cuyo resultado es el siguiente:




Corazón rojo en 2D

Cambiando los valores de la opción Thickness podemos variar la anchura del trazo.

Pero podríamos pedir más cosas. Cualquiera puede dibujar un corazón más o menos bien hecho y colorearlo entero de rojo (o de cualquier otro color). ¿Podemos nosotros? Pues claro que sí:

< < Graphics`FilledPlot` (para introducirlo en Mathematica quitad los espacios)
FilledPlot[{f[x],g[x]},{x,-2,2},Fills->{{{1, 2},RGBColor[1,0,0]}},Curves->None,AspectRatio->Automatic,Axes->False]

El resultado gráfico es el siguiente:



Corazón rojo relleno en 2D

¿A que es bonito? Pues aún hay más.

Amor en 3-D

Hemos dicho que todo el mundo puede dibujar un corazón en dos dimensiones más o menos decente y colorearlo de rojo, aunque hemos visto que con Mathematica el dibujo puede quedarnos mucho mejor. ¿Y si queremos dibujarlo en tres dimensiones? Parece más complicado. De hecho posiblemente a mucha gente le costaría mucho que su dibujo quedara mínimamente decente. Con Mathematica también podemos demostrar nuestro amor en 3-D. Además os voy a dar dos formas:

* Vamos a representar la superficie cuya ecuación implícita es:



Cargamos el paquete ContourPlot3D:

< < Graphics`ContourPlot3D` (quitadle los espacios)

Y dibujamos el corazón:

ContourPlot3D[(x^2+9/4 y^2+z^2-1)^3-x^2 z^3-9/80 y^2 z^3,{x,-3,3},{y,-3,3}, {z,-3,3},MaxRecursion->3,ViewPoint->{2.032,2.290,1.294},Axes->True,AxesLabel->{"Eje X", "Eje Y","Eje Z"}]

Obtenemos lo siguiente:



Corazón en 3D

Sí, ya lo sé, en rojo queda mucho mejor. Y sin ejes. Y si la caja. Vamos a ello:

ContourPlot3D[(x^2+9/4 y^2+z^2-1)^3-x^2 z^3-9/80 y^2 z^3,{x,-3,3},{y,-3,3},{z,-3,3},MaxRecursion->3,ViewPoint->{1,2.5,1}, Axes->False,LightSources->{{{0,0,1},RGBColor[1,0,0]}},Boxed->False]

Aquí lo tenemos:



Corazón rojo en 3D-1
* La segunda opción es representar la superficie cuya ecuación implícita es:



En este caso vamos a darlo directamente en rojo, sin ejes y sin caja. Para ello debemos tener ya cargado el paquete ContourPlot3D y ejecutar la siguiente orden en Mathematica:

ContourPlot3D[(2 x^2+y^2+z^2-1)^3-1/10 x^2 z^3-y^2 z^3,{x,-3,3},{y,-3,3},{z,-3,3},MaxRecursion->3,ViewPoint->{2.5,1,1}, Axes->False,LightSources->{{{0,0,1},RGBColor[1,0,0]}},Boxed->False]

Obteniendo así el corazón buscado:



Corazón rojo en 3D-2

Conclusión

Como podéis ver hemos conseguido nuestro objetivo: hemos conseguido que las matemáticas nos ayuden a demostrar nuestro amor a alguien. Por tanto podemos decir que hay funciones y ecuaciones que representar el amor, que lo llevan dentro, y que nos sirven para que mostremos el nuestro por alguien.


I Love Math

--------------------------------