Tartaglia y su Triángulo

Niccolo Fontana (1500 - 13 de diciembre 1557), matemático italiano apodado Tartaglia (el tartamudo) desde que de niño recibió una herida en la toma de su ciudad natal, Brescia, por Gastón de Foix. Huérfano y sin medios materiales para proveerse una instrucción, llegó a ser uno de los principales matemáticos del siglo XVI. Explicó esta ciencia sucesivamente en Verona, Vicenza, Brescia y finalmente Venecia, ciudad en la que falleció en 1557 en la misma pobreza que le acompañó toda su vida. Se cuenta que Tartaglia sólo aprendió la mitad del alfabeto de un tutor privado antes de que el dinero se agotara, y posteriormente tuvo que aprender el resto por su cuenta. Sea como sea, su aprendizaje fue esencialmente autodidacto.

Descubridor de un método para resolver ecuaciones de tercer grado, estando ya en Venecia, en 1535 su colega del Fiore discípulo de Scipione del Ferro de quien había recibido la formula para resolver las ecuaciones cúbicas, le propone un duelo matemático que Tartaglia acepta. A partir de este duelo y en su afán de ganarlo Tartaglia desarrolla la fórmula general para resolver las ecuaciones de tercer grado. Por lo que, consigue resolver todas las cuestiones que le plantea su contrincante, sin que éste logre resolver ninguna de las propuestas por Tartaglia.

El éxito de Tartaglia en el duelo llega a oídos de Gerolamo Cardano que le ruega que le comunique su fórmula, a lo que accede pero exigiéndole a Cardano jurar que no la publicará. Sin embargo, en vista de que Tarataglia no publica su fórmula, y que según parece llega a manos de Cardano un escrito inédito de otro matemático fechado con anterioridad al de Tartaglia y en el que independiente se llega al mismo resultado, será finalmente Cardano quien, considerándose libre del juramento, la publique en su obra Ars Magna (1570). A pesar de que Cardano acreditó la autoría de Tartaglia, éste quedó profundamente afectado, llegando a insultar públicamente a Cardano tanto personal como profesionalmente. Las fórmulas de Tartaglia serán conocidas como fórmulas de Cardano.

Quizás lo que más famoso ha hecho a este matemático es el conocido triángulo de números que lleva su nombre, a pesar de que también se conoce como Triángulo de Pascal: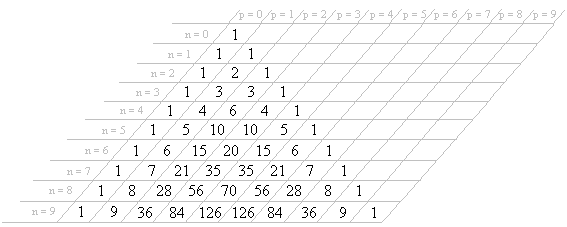



En él, cada número resulta de sumar los dos que haya en su extremo superior izquierdo y en su extremo superior derecho.

El Triángulo de Tartaglia está relacionado con los números combinatorios y con el desarrollo de las potencias de un binomio, como por ejemplo se puede apreciar aquí (los coeficientes del polinomio resultante coinciden con la fila n=4 del triángulo):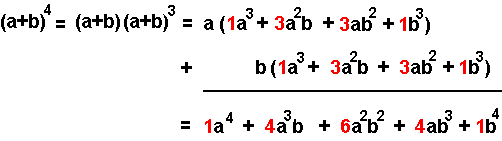




Así que ya saben, ya no tienen excusa para calcular "fácilmente" cualquier potencia de un binomio.


PD: El triángulo de Tartaglia encierra otras muchas propiedades curiosas, algunas de las cuales podéis ver aquí.


Fuente:

http://es.wikipedia.org/wiki/Tri%C3%A1ngulo_de_Pascal

http://es.wikipedia.org/wiki/Niccol%C3%B2_Fontana_Tartaglia

http://es.geocities.com/matesbueno/articulos/el_triangulo_de_tartaglia.htm